What Is RSA? A Complete Guide to Rivest–Shamir

RSA is one of the most widely adopted asymmetric encryption algorithms powering modern cybersecurity. It protects secure browsing, encrypted email, VPN connectivity, SSH authentication, API tokens, and nearly every certificate-based trust workflow online. When you access an HTTPS site or verify a software signature, RSA is working behind the scenes to protect your identity and ensure data confidentiality.

As cyber threats grow, RSA remains a key pillar of secure communications and Zero Trust identity frameworks. Understanding how RSA works is crucial for teams building secure cloud infrastructure and compliance-heavy enterprise applications.

What This Guide Covers

RSA definition explained simply and technically
RSA key generation + encryption/decryption workflow
Python and OpenSSL implementation examples
Enterprise and cloud-native real-world use cases
Best practices and common misconfigurations
Advanced applications aligned with Zero Trust

Workflow Diagram

1. What Is RSA?

RSA (Rivest–Shamir–Adleman) is a public-key cryptosystem built on asymmetric cryptography. It uses two mathematically linked keys:

Function	Who Uses It	Key
Encrypt or verify signatures	Anyone	Public Key
Decrypt or create signatures	Only the owner	Private Key

RSA security is based on the computational difficulty of factoring extremely large prime numbers. Even with modern compute, factoring a properly sized RSA modulus is impractical—making RSA resilient when used correctly.

Where RSA Is Used

SSL/TLS in HTTPS websites
SSH access for DevOps and remote admins
Code signing for software authenticity
Identity and access management systems
Machine-to-machine secure communication (APIs, IoT, services)

Who should care: Any organization that must secure identities, automation pipelines, and sensitive data.

2. Why RSA Matters Today

RSA continues to be essential, thanks to its:

Strong alignment with Zero Trust architecture
Wide support across legacy + cloud-native environments
Ability to validate identity using signatures
Compatibility with PKI workflows and certificate authorities
Role in secure key exchange during TLS handshakes
Stability and battle-tested cryptographic history

Even as quantum computing research advances, RSA remains critical in regulated industries—all the more reason to apply best-practice key sizes and crypto hygiene.

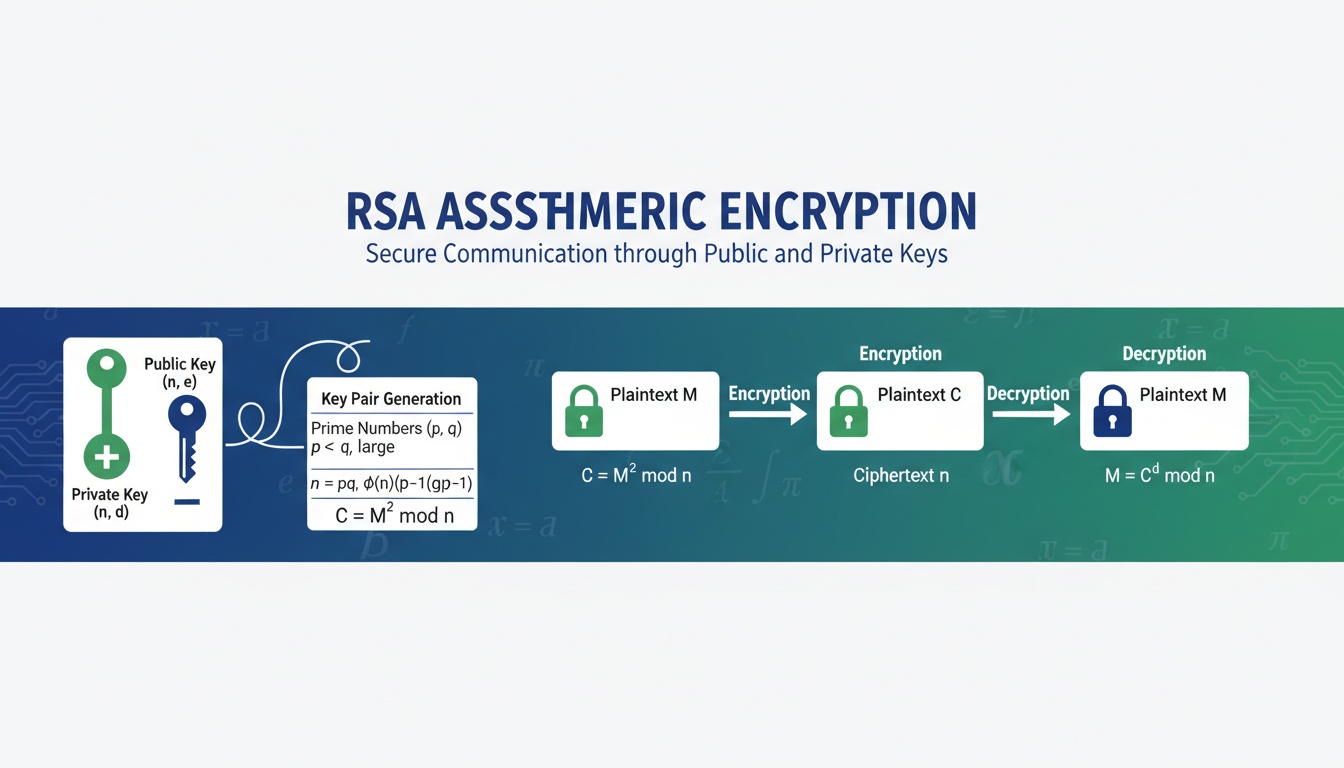
3. How RSA Works: Technical Deep Dive

RSA operations involve modular arithmetic and prime number theory. There are three core components:

Key Generation

Choose two large primes (p and q)
Compute modulus:
n = p × q
Calculate Euler’s totient:
φ(n) = (p – 1)(q – 1)
Select public exponent e (commonly 65537)
Compute private exponent d:
d = e⁻¹ mod φ(n)

The modulus n must remain un-factorable to attackers.

Public-Key Encryption

Plaintext message m
Ciphertext result:
c = mᵉ mod n
Public key enables encryption by anyone

Private-Key Decryption

Ciphertext value c
Computes plaintext:
m = cᵈ mod n
Only the key owner can decrypt

This asymmetric design enables trust even across untrusted networks.

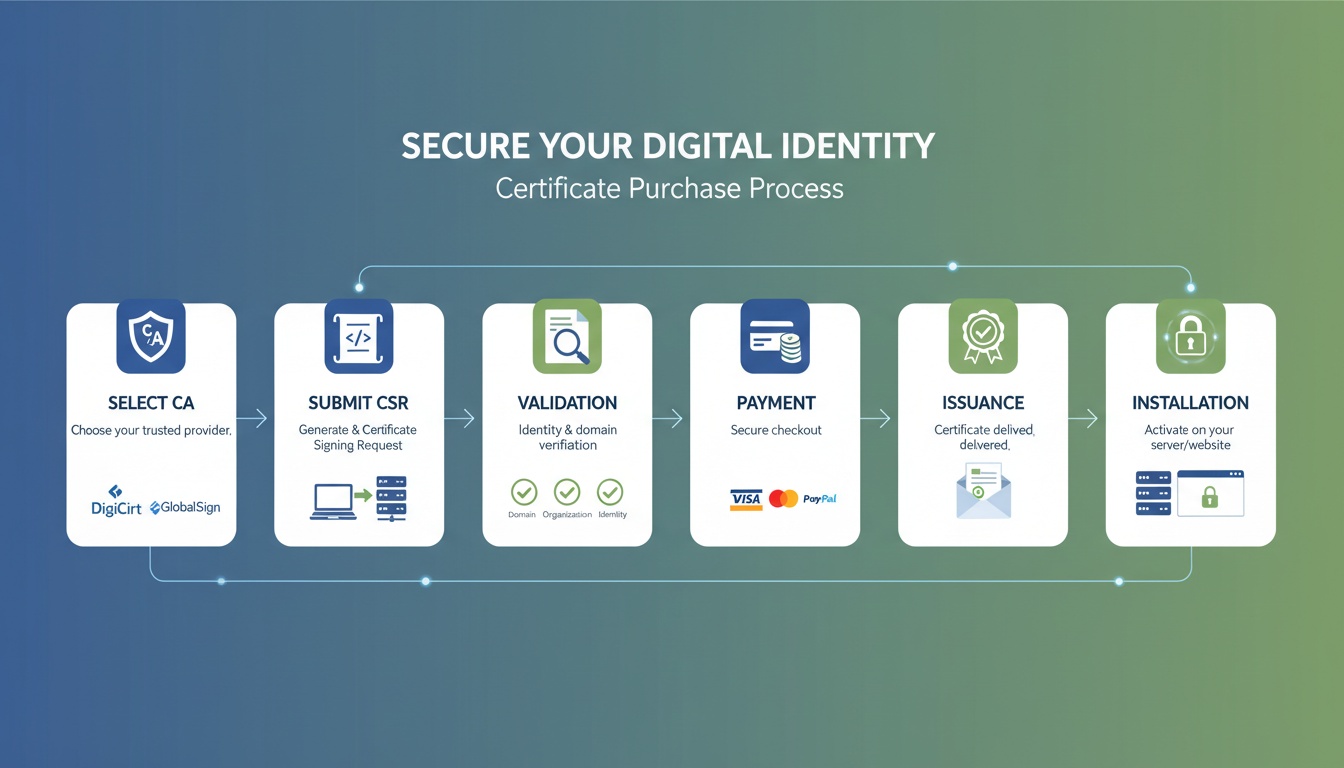
4. Step-by-Step RSA Workflow

Generate p & q (large primes)
Compute n = p × q
Calculate φ(n)
Choose e such that gcd(e, φ(n)) = 1
Compute private key d
Publish public key = (n, e)
Protect private key = (n, d)
Encrypt: c = mᵉ mod n
Decrypt: m = cᵈ mod n

5. Real Code Snippets

Generate RSA Keys with OpenSSL

openssl genpkey -algorithm RSA -out private.pem -pkeyopt rsa_keygen_bits:2048
openssl rsa -pubout -in private.pem -out public.pem

Encrypt & Decrypt in Python

from Crypto.PublicKey import RSA
from Crypto.Cipher import PKCS1_OAEP

key = RSA.generate(2048)
cipher = PKCS1_OAEP.new(key.publickey())

ciphertext = cipher.encrypt(b"hello rsa")
print(ciphertext)

decipher = PKCS1_OAEP.new(key)
plaintext = decipher.decrypt(ciphertext)

print(plaintext)

Signing & Verification in Python

from Crypto.Signature import pkcs1_15
from Crypto.Hash import SHA256

data = b"sign this securely"
hash_value = SHA256.new(data)

signature = pkcs1_15.new(key).sign(hash_value)
pkcs1_15.new(key.publickey()).verify(hash_value, signature)
print("Signature verified successfully")

6. Best Practices (Security Checklist)

Use RSA-2048 minimum; RSA-4096 for high compliance environments
Apply OAEP for encryption and PSS for digital signatures
Never store private keys in plain text or inside source code
Use HSMs or secure enclaves for private-key operations
Automate key rotation schedules
Use hybrid encryption (RSA + AES) for performance & scalability
Validate certificates using OCSP stapling
Disable outdated or weak 1024-bit keys immediately
Secure randomness during key generation
Protect private keys in transit (TLS + MFA)
Restrict access using role-based controls
Monitor certificate expiration to prevent outages
Audit key usage and maintain cryptographic governance

7. Common Pitfalls (Avoid These!)

Using RSA with no padding — catastrophic risk
Weak key generation caused by low entropy
Hard-coding keys into repositories
Re-using key modulus for multiple pairs
Relying solely on manual certificate renewals
Failing to validate signature verification logic
Continuing to use deprecated cipher suites

8. Advanced and Cloud-Native Use Cases

TLS handshake with RSA key exchange + identity validation
SSH identity for secure DevOps automation
Code signing (native apps, containers, firmware)
IoT device authentication and onboarding
Artifact integrity in CI/CD pipelines
API machine identity protection
Encrypted backup archives with key lifecycle governance
Mutual TLS (mTLS) for microservices security

9. Abbreviations & Cryptography Keywords (Explained)

This guide uses several security terms and acronyms. Here are their full forms and meanings:

Abbreviation / Term	Full Form / Explanation
RSA	Rivest–Shamir–Adleman — Asymmetric cryptographic algorithm based on large prime factorization
PKI	Public Key Infrastructure — Framework for managing digital certificates and keys
TLS	Transport Layer Security — Protocol that secures HTTPS and encrypted communication
SSL	Secure Sockets Layer — Older version of TLS (now deprecated but still referenced)
SSH	Secure Shell — Crypto-based secure remote access protocol
OAEP	Optimal Asymmetric Encryption Padding — Secure padding scheme for RSA encryption
PSS	Probabilistic Signature Scheme — Secure padding method for RSA digital signatures
HSM	Hardware Security Module — Tamper-resistant device for secure key storage
CA	Certificate Authority — Trust issuer for digital certificates
AES	Advanced Encryption Standard — Fast symmetric encryption algorithm used with RSA
ECC	Elliptic Curve Cryptography — Modern asymmetric cryptography using curve math
MFA	Multi-Factor Authentication — Uses additional identity verification factors
OCSP	Online Certificate Status Protocol — Real-time certificate revocation verification
CRL	Certificate Revocation List — Offline list of revoked certificates
Zero Trust	Security model requiring continuous identity validation and least-privilege access

These terms are essential to understanding how RSA enables secure identity, encryption, and trust in cloud and enterprise systems.

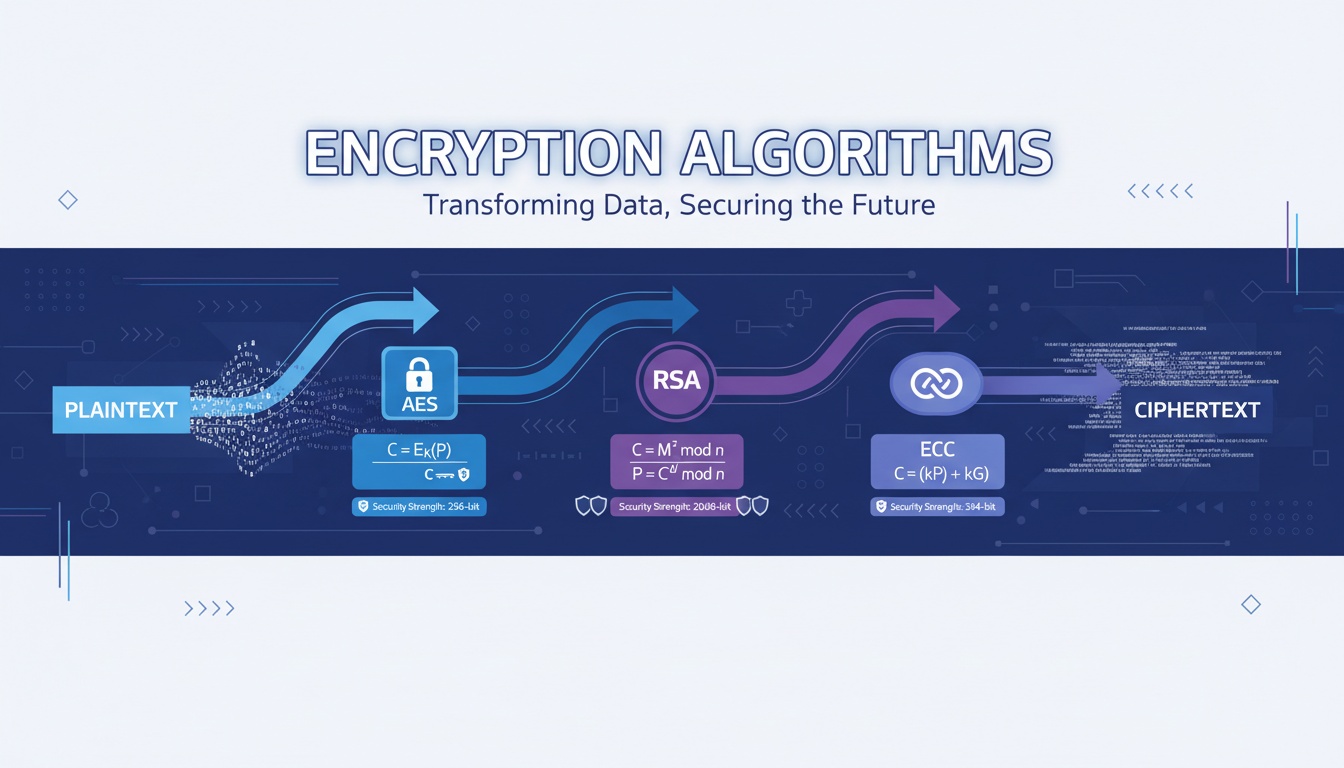
10. Cryptography Comparison Table

Feature	RSA	AES	ECC
Key Type	Asymmetric	Symmetric	Asymmetric
Performance	Slower	Very fast	Very fast
Key Size	2048–4096 bits	128–256 bits	256–521 bits
Primary Usage	Key exchange, signatures	Bulk data encryption	Lightweight secure comms
Security Basis	Large prime factorization	Block cipher strength	Elliptic curve algebra

Looking to Automate RSA Security in the Cloud?

Qcecuring helps you modernize PKI, SSH, SSL, and code-signing using secure automation. Book a Demo: https://qcecuring.com/request-demo

11. Final Summary

RSA secures authentication, encryption, and digital trust worldwide
It prevents unauthorized access by requiring private-key ownership
Prime-based mathematics make RSA hard to break using classical computing
Enterprises depend on RSA for certificates, identity, and compliance
When combined with automation, RSA enables Zero Trust security at scale

What Is RSA? A Complete Guide to Rivest–Shamir–Adleman Cryptography